一直追老黄的剧本的小伙伴就知道老黄为什么要写这篇文章,来龙去脉尽在前三篇作品中。有兴趣的小伙伴可以回阅老黄前三篇关于高数的作品。或者单看下面的问题也是可以的。但可能会错失比较多东西。
已知函数f(x)及其导函数f’(x)的定义域均为R,akp≠0,
(1)若f’(x)+kf(x)=asinpx, 求f(x);
(2)若f’(x)+kf(x)=acospx, 求f(x).
f'(x)+kf(x)的形式,老黄就称之为“线性和”。这个原函数f(x)的通解是有公式的。老黄之前求过它的特例k=-1的形式。但是发现不够用,需要k=-2的形式,才能解决老黄最终想解决的问题(网友分享的一道k8联考的高数难题的第二种解法)。
因此以老黄的脾气,干脆就推导出它的普遍形式,免得k取不同的值都要重新推导一遍公式,那也未免太麻烦了。不过由于有前面推导过程给的启发,解决这个问题就有了依据,变得相对简单了许多。要是没有前面的经验,想解决这个问题还真不是很容易哦。以下是老黄前面推导的过程,用图片形式分享如下:

上图只有关于正弦的公式,关于余弦的公式,老黄是在例题和练习中直接给出的。这里就不同了,不只有关于正弦的公式推导,也有关于余弦的公式推导。
解:(1)记*f(x)=hcospx+jsinpx,h,j是常数.【老黄以*f的形式,表示公式的特解。前面还有一部分是Ce^(-kx),两个部分的和构成通解】
则*f’(x)=-phsinpx+pjcospx.【对特解求导,那么两者与题干相同的线性和,结果应该不变。因为前面部分Ce^(-kx)与它的导数互为相反,和等于0。由这个原理列得如下关于h,j的方程式】
从而有{kj-ph=a;pj+kh=0};解得:(h=-ap/(k^2+p^2); j=ak/(k^2+p^2)),
∴f(x)=Ce^(-kx)-apcospx/(k^2+p^2)+aksinpx/(k^2+p^2). 【这就是第(1)个微分方程的通解公式了,由于sin(px+b)中的常数b对结果不造成影响,所以这个公式可以拓展为】
若f’(x)+kf(x)=asin(px+b), 则
f(x)=Ce^(-kx)-apcos(px+b)/(k^2+p^2)+aksin(px+b)/(k^2+p^2).

(2)acospx=asin(px+π/2),【转化为第(1)小题的形式】
由(1)有, f(x)=Ce^(-kx)-apcos(px+π/2)/(k^2+p^2)+aksin(px+π/2)/(k^2+p^2).【现求现用好愉快】
∴f(x)=Ce^(-kx)+apsinpx/(k^2+p^2)+akcospx/(k^2+p^2).【这就是第(2)个微分方程的通解公式了,同理也可拓展为】
若f’(x)+kf(x)=acos(px+b), 则
f(x)=Ce^(-kx)+apsin(px+b)/(k^2+p^2)+akcos(px+b)/(k^2+p^2).

这两个公式,比老黄上一次推出来的关于整式的公式,要简单得不是一星半点,用起来也容易得多的n次方。比如下面这道例题:
若y’-2y=3sin(2x-π/3), 求y.
解:f(x)=Ce^(-kx)-apcos(px+b)/(k^2+p^2)+aksin(px+b)/(k^2+p^2)【不熟练的情况下,就把公式写下来。这里k=-2, a=3,b=-π/3, p=2,一骨脑代入公式就可以了】
=Ce^(2x)-3/4*cos(2x-π/3)-3/4*sin(2x-π/3).
这个结果老黄已经检验过了,完全正确的。
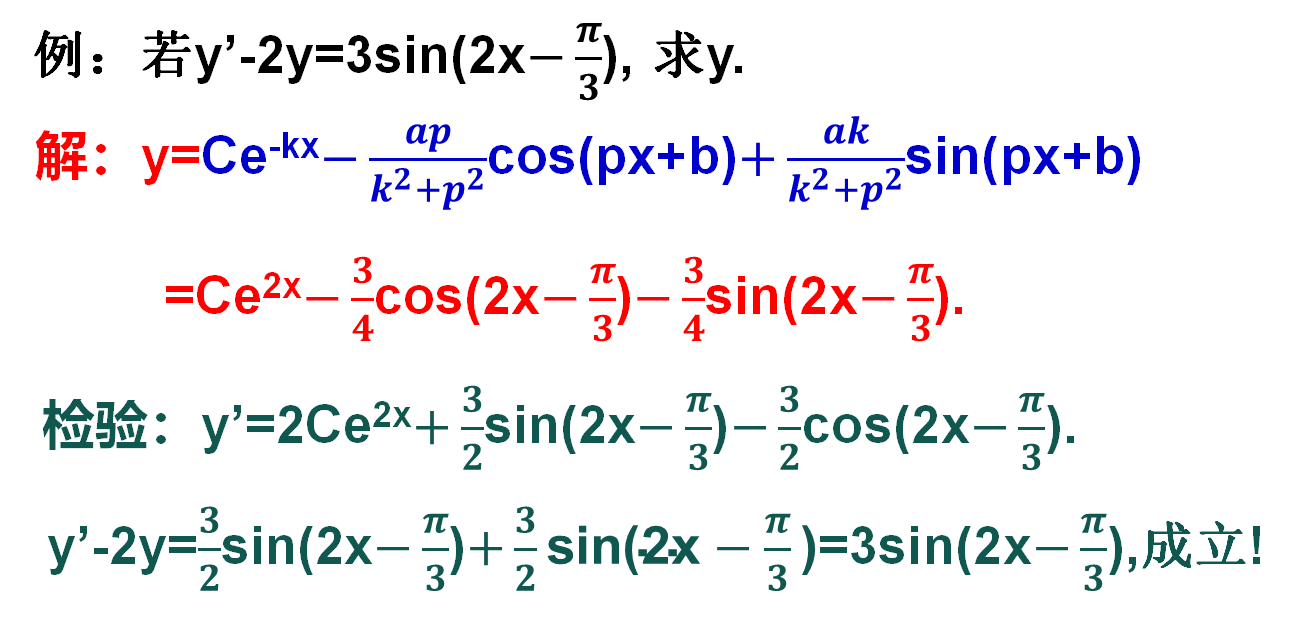
再看一道练习:若2y’+y=3cos4x, 求y.
这回直接给图片形式的答案如下:(关键是第一步,要把方程化成公式条件的一般形式)
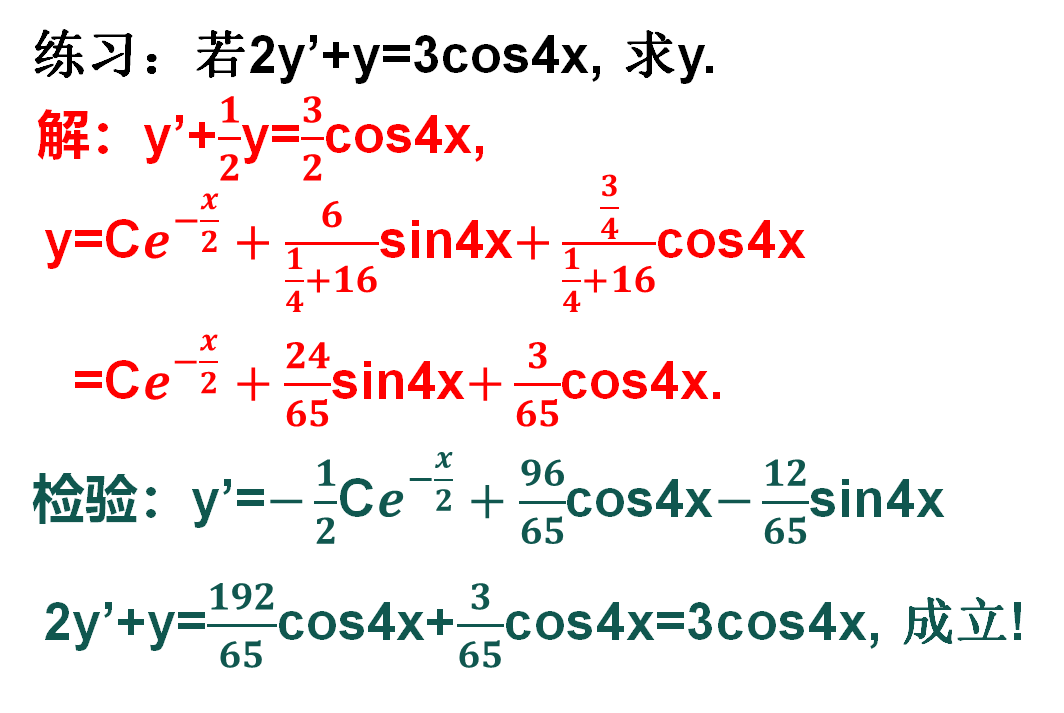
最后再把两个公式整理一下,特别地写出当a=p=1, b=0的形式。因为老黄后面的作品要用到它们。

